Clase 6

 EDGAR VALDEZ

202306010

6TA CLASE

ESTADISTICA

Probabilidad condicional e independencia

El concepto de probabilidad condicional está presente en el habla cotidiana. Son comunes, por ejemplo, expresiones del tipo:

Cuando llueve, la probabilidad de que se produzcan atascos es del 40%.

Si 

$A$

 es el evento atascos, la expresión anterior no significa que 

$P\left(A\right)=.4$

: 

$A$

 incluye también el evento atasco en ausencia de lluvia. Si 

$B$

 es el evento lluvia, la manera en que se representa la expresión anterior es

$$P\left(A|B\right)=.4,$$

que se lee así: la probabilidad condicional de 

$A$

 dado 

$B$

 es del 40%.

Supóngase ahora que de cada 100 días, 10 llueve. Es decir, que 

$P\left(B\right)=.1$

. Entonces, de cada 100 días, 4 lloverá y habrá atasco. Es decir, 

$P(A\cap B)=0.04$

. En general,

$$P(A\cap B)=P\left(A|B\right)\times P\left(B\right)$$

o, como se suele ver escrito por todas partes,

$$P\left(A|B\right)=\frac{P(A\cap B)}{P\left(B\right)}$$

.$$P(A|B)=\frac{P(A\cap B)}{P(B)}.$$

Ejercicio 3.1 Supóngase que 

$P\left(A\right)=.2$

 y 

$P\left(B\right)=.5$

. Entonces, ¿cuáles de las siguientes afirmaciones son necesariamente ciertas?

• $P\left(A|B\right)=.1$
• $P\left(A|B\right)\le .4$
• $P\left(A|B\right)>0$

¿Puedes ilustrar tu razonamiento con ejemplos concretos y cotidianos?

El concepto de la probabilidad condicional aparece en muchos contextos, frecuentemente con denominaciones específicas. Por ejemplo, en epidemiología se distingue entre la tasa de mortalidad (o la probabilidad de morir a causa de una determinada enfermedad), que podríamos representar como 

$P\left(M\right)$

 y la tasa de letalidad, 

$P\left(M|C\right)$

, que es la probabilidad de morir condicionada a haber contraído la enfermedad. También se habla de tasa de paro (la probabilidad de estar desempleado) y, p.e., tasa de paro femenina, o la probabilidad de que una mujer se encuentre desempleada, que es la probabilidad de que una persona esté desempleada condicionada a que dicha persona es mujer (o 

$P\left(D|M\right)$

).

Hablar de probabilidades condicionales viene a ser equivalente a cambiar (o estrechar) el marco de referencia, el evento total. De hecho, por lo anterior,

$$P\left(B|B\right)=\frac{P(B\cap B)}{P\left(B\right)}$$

=P(B)P(B)

=1.$$P(B|B)=\frac{P(B\cap B)}{P(B)}=\frac{P(B)}{P(B)}=1.$$

Al condicionar por 

$B$

, por lo tanto, se está reemplazando el conjunto total, 

$\Omega$

, por 

$B$

. En el ejemplo concreto con el que se inicia esta sección, eso significa que ya no se tienen en cuenta todas las condiciones meteorológicas posibles sino solamente aquellas en que llueve.

Ni que decir tiene que también es posible condicionar usando eventos definidos por variables aleatorias. En tal caso, por abreviar, se usa la notación

$$P(A|X=a)$$

para representar la probabilidad de 

$A$

 condicionada por evento en que la variable aleatoria 

$X$

 toma el valor 

$a$

. También se usan otras expresiones análogas cuyo significado se entenderá sin problemas en su contexto.

Probabilidad condicional para sucesos independientes

Dos sucesos,  y , son independientes cuando la probabilidad de que suceda  no se ve afectada porque haya sucedido, o no, .

Por ejemplo, Si tiramos dos veces una moneda, el segundo resultado que obtenemos no está influenciado por el primer resultado obtenido.

Si dos sucesos  y  son independientes, entonces .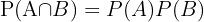

Por tanto, si , de la definición de probabilidad condicional resulta que:

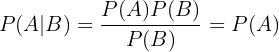
En otras palabras, si dos sucesos  y  son independientes, entonces la probabilidad condicional de  cuando se sabe que  ha ocurrido es la misma que la probabilidad incondicional de  cuando no se dispone de información sobre . El resultado recíproco también es cierto, si:

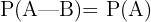
entonces los sucesos  y  deben ser independientes.

Sucesos dependientes

Dos sucesos,  y , son dependientes cuando la probabilidad de que suceda  se ve afectada porque haya sucedido, o no, .

Dos sucesos  y  son dependientes si:

Fuente: https://www.youtube.com/watch?v=Q6QYG2VtdMA

Fuente: https://www.youtube.com/watch?v=AT78AzlPjnM

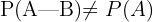
Ejemplo de probabilidad condicional

A continuación, veamos un ejemplo de probabilidad condicional.

Supongamos que tenemos un aula con 30 alumnos, siendo el 50 % de 14 años y el otro 50% de 15 años. Además, sabemos que 12 integrantes del salón tienen 14 años y usan resaltador en sus libros ¿Cuál es la probabilidad de que un estudiante del salón use resaltador si tiene 14 años?

Siguiendo la fórmula mostrada líneas arriba, primero, sabemos que la probabilidad de que el estudiante tenga 14 años es 50%(P(B)). Asimismo, la probabilidad que de que un estudiante tenga 14 años y use resaltador es 12/30=40%.

Por lo tanto, la probabilidad de que un estudiante use resaltador si tiene 14 años se calcularía de la siguiente forma:

P(A|B)=P(A ∩ B)/P(B)=0,4/0,5=0,8=80%

Es decir, existe un 80% de probabilidad de que un estudiante use resaltador si tiene 14 años.

Propiedades de la probabilidad condicional

Las propiedades de la probabilidad condicional son las siguientes:

• 

La suma de la probabilidad de A dado B y la de su complemento dado B es 1, cubriendo todas las posibilidades.

• 

Si A está dentro de B o son iguales, la probabilidad de A dado B siempre es 1, indicando certeza.

• 

Lo anterior quiere decir que la probabilidad de A es igual a la probabilidad de A dado B por la probabilidad de B más la probabilidad de A, dado el complemento de B por el complemento de B.

fuente:https://economipedia.com/definiciones/probabilidad-condicional.html#google_vignette