Edgar Valdez
202306010
clase 9
en esta clase solo le tocó a un grupo pasar a exponer los integrantes fueron elegidos por el Ingeniero y estos fueron Sofonías y Elena el tema que impartieron fue el de
La diferencia entre el Teorema de la Probabilidad Total y el Teorema de Bayes
Seguramente te suenen del curso de Estadística y Probabilidad, dos de los teoremas más importantes de esta
área: el Teorema de la Probabilidad Total y el Teorema de Bayes.
Sin embargo, muchas veces puede ocurrir que no se acabe de entender muy bien cuándo hablamos de uno
o de otro, en qué se parecen y en qué se diferencian, y lo más importante, para qué sirven. Así que en el post
que les traigo hoy vamos a
hablar de todo ello a ver si le damos un poco más de luz al asunto.
Teorema de la Probabilidad Total
Este teorema permite hallar la probabilidad de un evento B cuando el espacio muestral Ω está dividido en
varios eventos: A1, A2, A3, …, An.
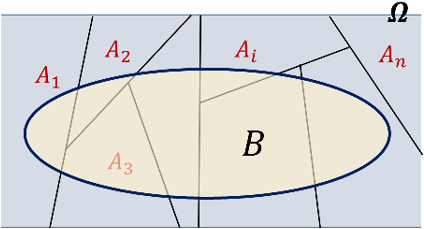
Si observamos la imagen anterior, tiene lógica que se le llame Teorema de la Probabilidad Total, ya que vemos
que realmente el evento B se puede expresar como la suma de todos los trocitos en los que se intersecta con
los eventos Ai.
De ahí que la fórmula se plantee de la siguiente manera:
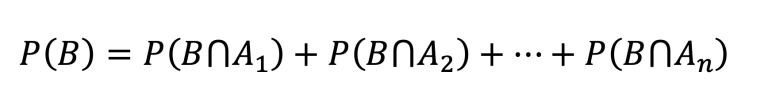
Luego, teniendo en cuenta la fórmula de la probabilidad condicional:
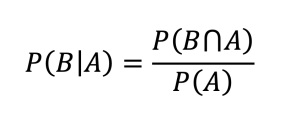
Si miramos bien la última fórmula de arriba, y despejamos la probabilidad de la intersección, podemos sustituir
cada intersección en la fórmula de la P(B), por un producto entre una probabilidad condicional y la probabilidad
de cada Ai:
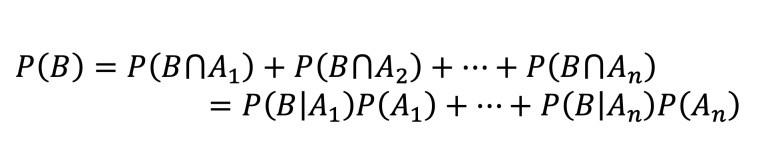
Veamos un ejemplo donde pondríamos en práctica el Teorema de la Probabilidad Total.
En una sala de pediatría de un hospital, el 60% de los pacientes son niñas, y el 40% son niños. De los niños el
35% son menores de 24 meses. Y de las niñas el 20% son menores de 24 meses. Un pediatra que ingresa a
la sala selecciona un infante al azar. Determina la probabilidad de que el infante seleccionado sea menor de 24
meses.
Lo primero que tenemos que ver es que nos interesa el evento B = «infante menor de 24 meses» y que el
espacio muestral (los infantes de la sala de pediatría) está dividido en dos partes: A1 = «niñas» y A2 = «niños».
Nos piden la probabilidad P(B), la probabilidad de que un infante seleccionado al azar sea menor de 24 meses.
Así que tenemos que tener en cuenta tanto a los niños menores de 24 meses como a las niñas menores de 24
meses, así como la cantidad (o porcentaje) de niños y niñas en general en la sala de pediatría:
Teorema de Bayes
El teorema de Bayes es útil para encontrar una probabilidad condicionada de un suceso cuando ya ha ocurrido
otro suceso que afecta la probabilidad del primer suceso. Siguiendo el ejemplo anterior, si el infante seleccionado
resulta ser menor de 24 meses, ¿cuál sería la probabilidad de que sea una niña? Es decir me piden P(A1|B).
Para lo cual aplicamos la siguiente fórmula:
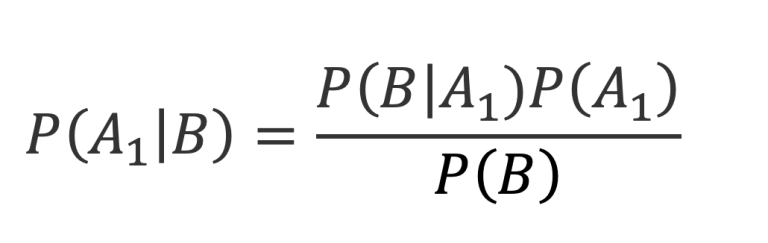
Si te fijas, el numerador es muy sencillo de calcular porque ya tenemos esos datos, y además es equivalente a
P(B∩A1). Mientras que el numerador ya lo tenemos calculado con el Teorema de la Probabilidad
Total. Entonces quedaría:
Entonces quedaría:
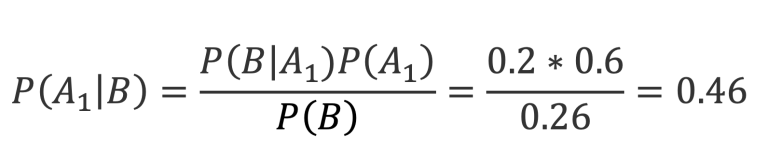
No hay comentarios:
Publicar un comentario